Terug naar de hoofdpagina uitwerkingen
Uitwerkingen les 3
Opgave 1
$L_k = 15,7\ cm$
$t_M = 0,46\ min$
opgave a:
$t_R\ component\ a = t_{Ra} = 5\ min$
$t_R\ component\ b = t_{Rb} = 12,2\ min$
$t_Rβ = t_R - t_M$
Dus:
$t_{Ra}β = 5 - 0,46 = 4,54\ min$
en
$t_{Rb}β = 12,2 - 0,46 = 11,74\ min$
opgave b:
$π^β²=\frac{π‘_π
βπ‘_π}{π‘_π} = \frac{π‘β²_π
}{π‘_π}$
dus:
Voor component a:
$π_aβ=\frac{5β0,46}{0,46} = \frac{5}{0,46} = 9,87$
Voor component b:
$π_bβ=\frac{12,2β0,46}{0,46} = \frac{11,74}{0,46} = 25,52$
opgave c:
$\alpha =\frac{(π‘_π
)_π΅βπ‘_π}{(π‘_π
)_π΄βπ‘_π}$
dus:
$\alpha =\frac{(π‘_π
)_π΅βπ‘_π}{(π‘_π
)_π΄βπ‘_π} = \frac{(tβ_R)_B}{(tβ_R)_A} = \frac{kβ _B}{kβ_A} = \frac{25,5}{9,87} = 2,59$
opgave d:
Omzetten van een fysieke afstand op papier (in cm) naar tijd (in min) $10\ min = 4,9\ cm$
let op: deze waarde kan verschillen van jouw opgemeten waarden maar de verhouding blijft altijd gelijk!
Gemeten:
$W_A = 2,1\ cm$
$W_B = 2,0\ cm$
dus:
$W_A = \frac{10 \cdot 2,1}{4,9} = 4,29\ min$
$W_B = \frac{10 \cdot 2,0}{4,9} = 4,08\ min$
opgave e:
$π=16\cdot\left(\frac{π‘_π
}{π}\right)^2$
Voor component A:
$π_A=16\cdot\left(\frac{π‘_π
}{π}\right)^2 = 16 \cdot \frac{5}{4,29} = 21$
Voor component B:
$π_B=16\cdot\left(\frac{π‘_π
}{π}\right)^2 = 16 \cdot \frac{12}{4,08} = 138$
Gemiddeld aantal schotels:
$\overline N = \frac{21 + 138}{2} = 79\ schotels$
opgave f:
Aantal schotels per meter:
$N_{per\ meter} = \frac{N}{l (m)} = \frac{79}{0,157} = 503\ schotels/m$
opgave g:
Gemiddelde Schotel hoogte:
$H = \frac{L}{\overline N} = \frac{15,7}{79} = 0,199\ cm$
opgave h:
Resolutie:
$R_S = \frac{2 \cdot (t_{R,B} - t_{R,A})}{W_A + W_B} = \frac{2 \cdot (12,2 - 5)}{4,29 + 4,08} = 1,72$
opgave 2
opgave a, b en c:
Zie Excel file
opgave d:
$\overline N = \frac{1024 + 435 + 355 + 238}{4}=513$
opgave e:
Aantal schotels per meter:
$N_{per\ meter} = \frac{N}{l (m)} = \frac{513}{0,35} = 1466\ schotels/m$
opgave f:
$\overline H = \frac{L}{N}=\frac{0,35}{513}=0.00068\ m=0,68\ mm$
opgave g:
$R_S = \frac{2 \cdot (t_{R,B} - t_{R,A})}{W_A + W_B}$
Zie Excel file
Opgave 3
opgave a
$R_S = \frac{2 \cdot (t_{R,B} - t_{R,A})}{W_A + W_B}$
$R_S = \frac{2 \cdot (4,8 - 2,9)}{0,35 + 1,04} = 2,73$
opgave b
$\alpha =\frac{(π‘_π
)_π΅βπ‘_π}{(π‘_π
)_π΄βπ‘_π}$
dus:
$\alpha =\frac{4,8-1,4}{2,9-1,4} = 2,27$
opgave c
We nemen aan dat de selectiviteit en capaciteit gelijk blijven.
Er is een lineair verband tussen het aantal schotels en de lengte van een kolom.
De resolutie is proportioneel aan de wortel van het aantal schotels en daarom ook aan de wortel van de lengte van de kolom.
Als we nu de volgende formule:
$R_s = \frac{\sqrt{N}}{4}\cdot\frac{\alpha-1}{\alpha}\cdot\frac{kβ_b}{1 + kβ_b}$
sterk vereenvoudigen tot:
$R_s = \sqrt{N}$
Aantal schotels was proportioneel met de lengte dus:
$R_s = \sqrt{L}$
ofwel:
$L = {R_s}^2$
Met verhoudingen werken:
$\frac{L_1}{L_2} = \frac{R_{S1}^2}{R_{S2}^2}$
$\frac {31,8}{L_2} = \frac{2,73^2}{1,5^2}$
$2,73^2 \cdot L2 = 31,8 \cdot 1,5^2$
$L2 = 9,6\ cm$
opgave d
Deze opgave is ook op te lossen door met verhoudingen te werken:
Er is een lineair verband tussen de resolutie en retentietijd.
Dus:
$\frac{t_{R1}}{t_{R2}} = \frac{R_{S1}}{R_{S2}}$
$\frac{4,8}{t_{R2}} = \frac{2,73}{1,5}$
$2,73 \cdot t_{R2} = 4,8 \cdot 1,5$
$t_{R2} = 2,64\ min$
opgave 4
opgave a
De pieken van componenten met een normale verdeling zijn lineair ofwel helium, krypton en argon.
Niet lineair is fluorine. Deze piek vertoont tailing.
opgave b
- De te bepalen analyt heeft een sterkere affiniteit met het oplosmiddel dan met de mobiele fase
- Interactie tussen amines en vrij silanol in de stationaire fase
- Interactie van zuren met de silica
- Een lege ruimte in de pakking van de kolom (dood volume)
opgave c
Helium: Cs uitgezet als functie van Cm:
Lijn loopt recht. Geen voorkeur.
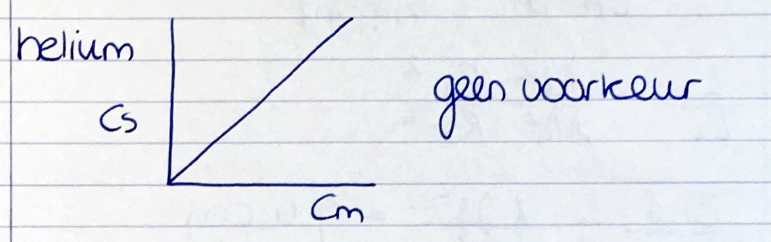
Fluorine: Cs uitgezet als functie van Cm:
Lijn loopt convex. Voorkeur voor stationaire fase.
Opgave 5
opgave a
Zie figuur blz. 204 boek.
opgave b
De A term (Eddy diffussie\ook wel βmultiple pathsβ genoemd).
opgave c
- Longitidunale diffussie ofwel de
B term. - Massa transport ofwel de
C term. Wordt ook wel de transportweerstand of evenwichtintstelling (equilibration time) genoemd.
opgave d
Longitidunale diffussie (b-term) heeft bij vloeistofchromatografie weinig invloed. Mobiele fase is een vloeistof. Bewegingssnelheid is klein vergeleken met een gas.
opgave e
Bij een lage $\mu$ (flow rate) speelt de longitidunale diffussie wel een grote rol. Er is immers veel tijd voor. De B-term is daarbij dus heel erg hoog.
$H = A + \frac{B}{\mu}+ C \mu$
Als B heel erg hoog is en $\mu$ heel laag dan wordt de breuk $\frac{B}{\mu}$ een groot getal.
Zodoende wordt H erg hoog.
opgave f
Bij een hoge $\mu$ (flow rate) speelt massa transport een grote rol (veel uitwisseling tussen mobiele en stationaire fase). De C-term is daarbij dus heel erg hoog. Hierdoor wordt H ook hoog.
De C-term kan laag gehouden worden door kleine particles te gebruiken en de kolom goed vol te pakken met de particles.
Opgave 6
opgave a
Voorwaarden interne standaard:
- Chemisch gelijksoortig aan glucose
- Ongeveer dezelfde concentratie gebruiken
- Niet gelijk elueren met glucose
opgave b
$C_S = 12,46\ mg\ fructose/25\ ml$
$C_S = 0,498\ mg/ml$
$C_m = \frac{A_m}{A_{IS,\ m}} \cdot \frac{A_{IS,\ std}}{A_{std}}\cdot C_S$
Let op dat de concentraties fructose en glucose niet gelijk zijn.
Hier dient een correctie op plaats te vinden.
dus:
$C_m = \frac{A_m}{A_{IS,\ m}} \cdot \frac{A_{IS,\ std}}{A_{std}}\cdot \frac{C_{std}}{C_{IS, std}}\cdot C_S$
$C_m = \frac{5,97}{6,38}\cdot \frac{4,37}{10,86}\cdot \frac{1,03}{1,16}\cdot 0,498 = 0,167\ mg/ml$
Opgave 7
opgave a
Eerste rij uiteraard geen zuur. Zie dus vanaf rij 2.
opgave b
Zie Excel file
opgave c
Externe standaard methode.
opgave d
Zie Excel file
Propionzuur is niet terug gevonden.
opgave e
Zie Excel file
opgave f
Zie Excel file